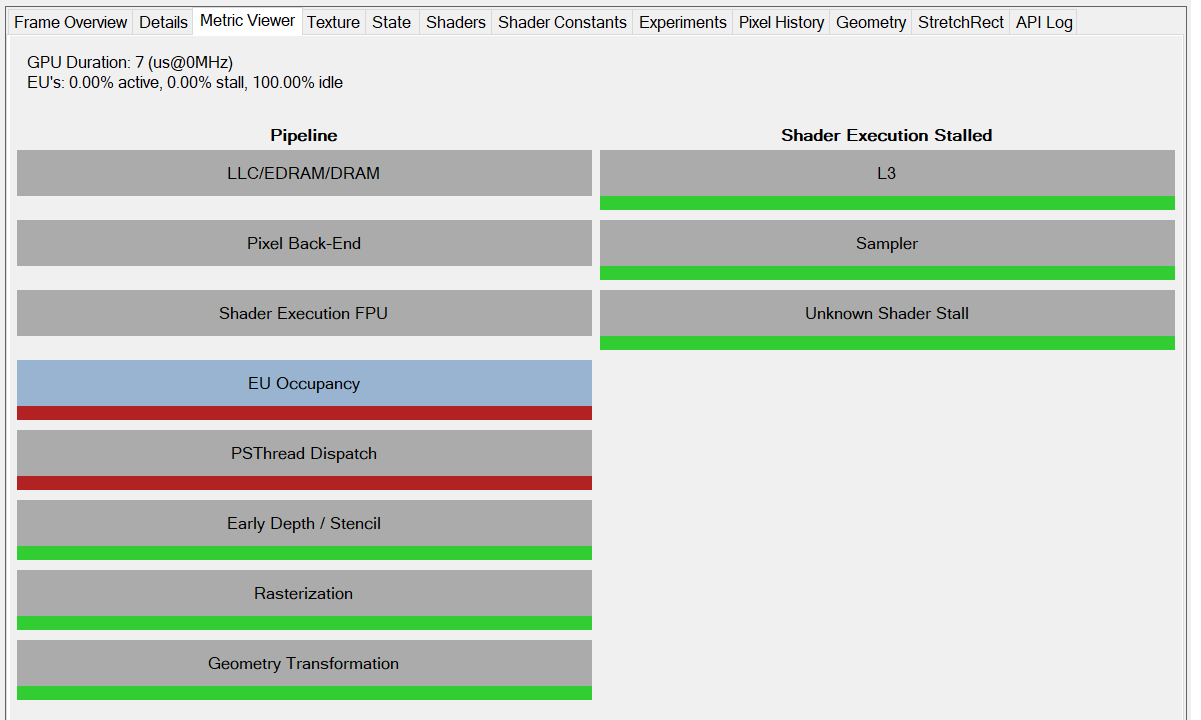
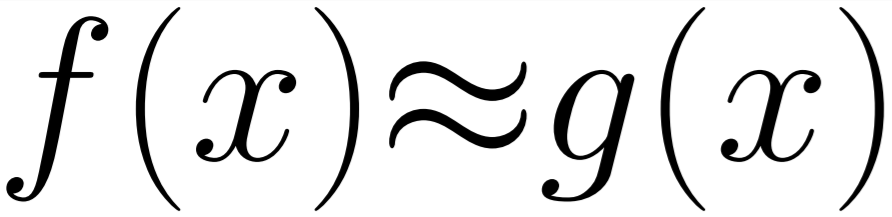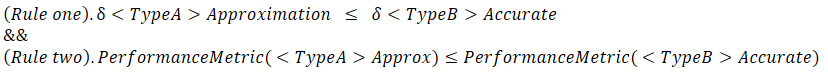We can see in this image that the depth buffers used for the shadow map are still bound and cleared each frame (RT2-5) and are apparently unused, but I may have missed something.
Sins of a Render Empire
So in the last three sections I gave an overview of the pipeline and how it changes in different configurations - essentially some features are disabled as LOD features based on distance. However, this isnt the only place to look when we are considering performance. So in this section we are going to cover a few oddities that need addressing if this game was going to be optimised.
4k Support
As I mentioned in the setup for this, I intended to run this on max setting at 4k resolution. This currently isn't possible with a high-end intel chip and NVidia 1080 - a little strange for a game from 2013.
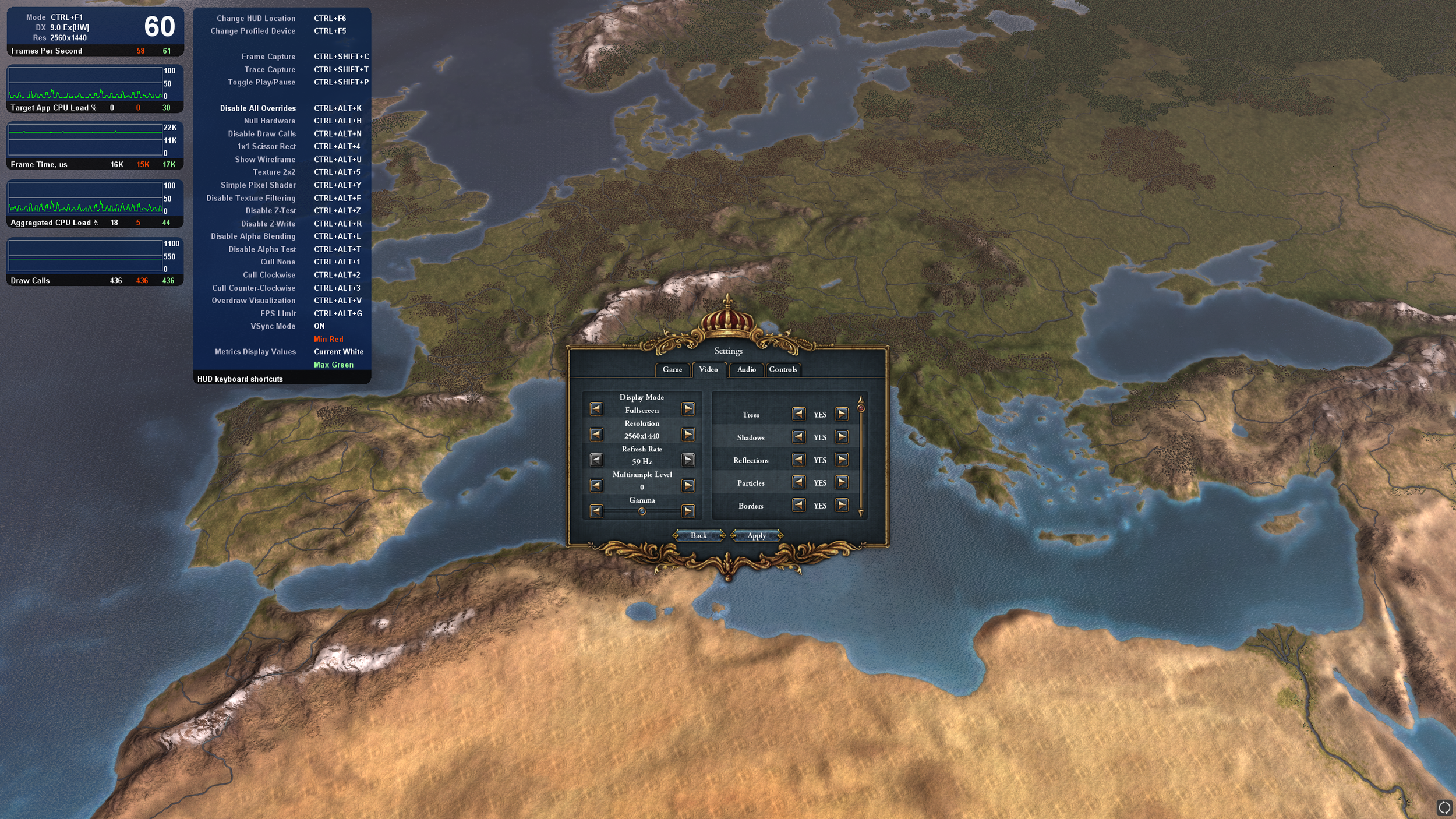
The game runs roughly fine at 4k when we dont enable all the on-off options in the video menu. A quick investigation into this and it seemed that the shadows really take most the time. A problematic quirk of resolutions is that when we double the size we quadruple the number pixels (which also quadruples the amount of work). In this engine, the shadow buffers appear to be sized based on the full rendering resolution. So, going from 1440p to 4k doesnt just quadruple the cost of rendering the scene, it has to be rendered twice at that size, so it is a ~8x increase in rendering cost.
Additionally the trees are expensive at 4k. This is a relatively simple reason, at 4k we see more pixels on each tree. Each tree has high texture detail and for some reason a detailed normal map. So now we have also quadrupled the texture read cost, with little coherency because the trees are small and dense and the texture resolution is reasonably high.
Water is similarly effected, but not as much as the trees due to similarity in the pixel space helping cache coherency.
In the game there are a number of what appear to be generated textures, the size of these appears to be loosely based on the resolution that is being used. However, they do not stick to power of two texture sizes. So a texture that is 1029x1029 is actually a 2048x2048 texture under the hood on certain hardware, this doesnt effect the appearance of the texture but does have performance implications and is just a massive waste of memory.
This next complaint is just because I play this game a lot. At 4k the menus get really tiny and that's a pain.
DirectX 9.0c
This game is written with DirectX 9.0c. In 2013 when this came out, DirectX 10 and 11 had long been a standard and DirectX 12 was well on the way as well as AMD's early experiments with Mantle which led to Vulkan.
AMD and NVIDIA put a lot of work into optimising drivers for modern hardware. This focus is obviously for patterns and use-cases in common software. DirectX 9.0c misses a lot of features that could really make this type of game fly on even a basic laptop.
Overbinding and draw calls
Textures are bound each time they are used. Tiny objects are submitted to draw calls. There is either a massive lack of batching or it is not apparent in the capture.
This puts the game at the mercy of the PCI-bus and the drivers. Every time you ask the GPU to do something you risk a major state change stalling the next draw. So much of the textures being bound are identical (outside of the UI) and there is a lot of texture slots to bind, some textures are so low resolution they may as well be constant buffers and allow for some nice out of order operations to be able to be done.
Texture Space Wastage
The cubemap for the sea is a good example of this. Due to the angle of the camera only a limited section of the cubemap will be accessed, so half of the cube map is just blank. This is more likely a trade-off than an error as the DX9 cubemaps have some strange rules - but it isn't ideal in a modern game.