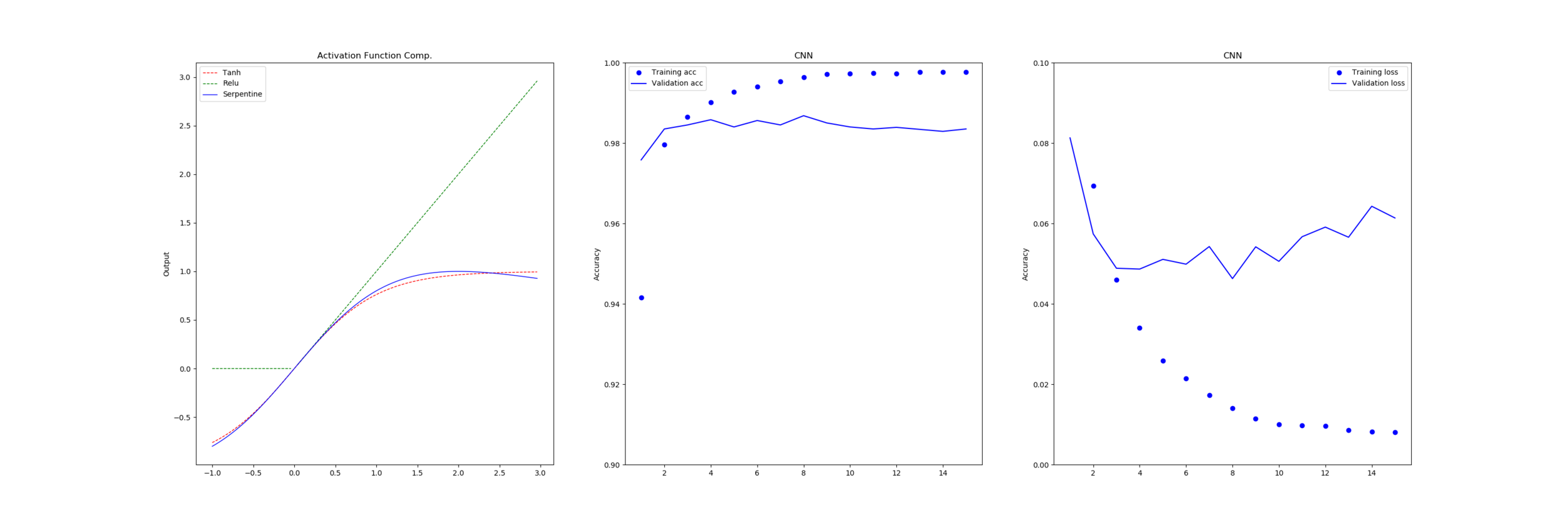
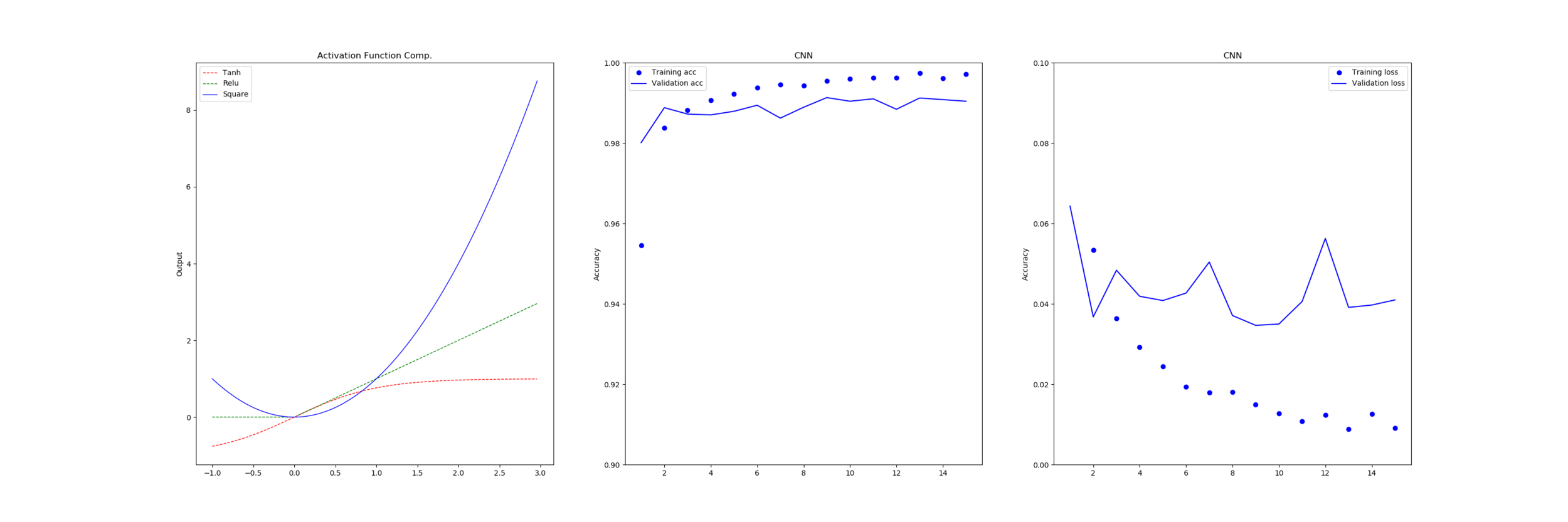
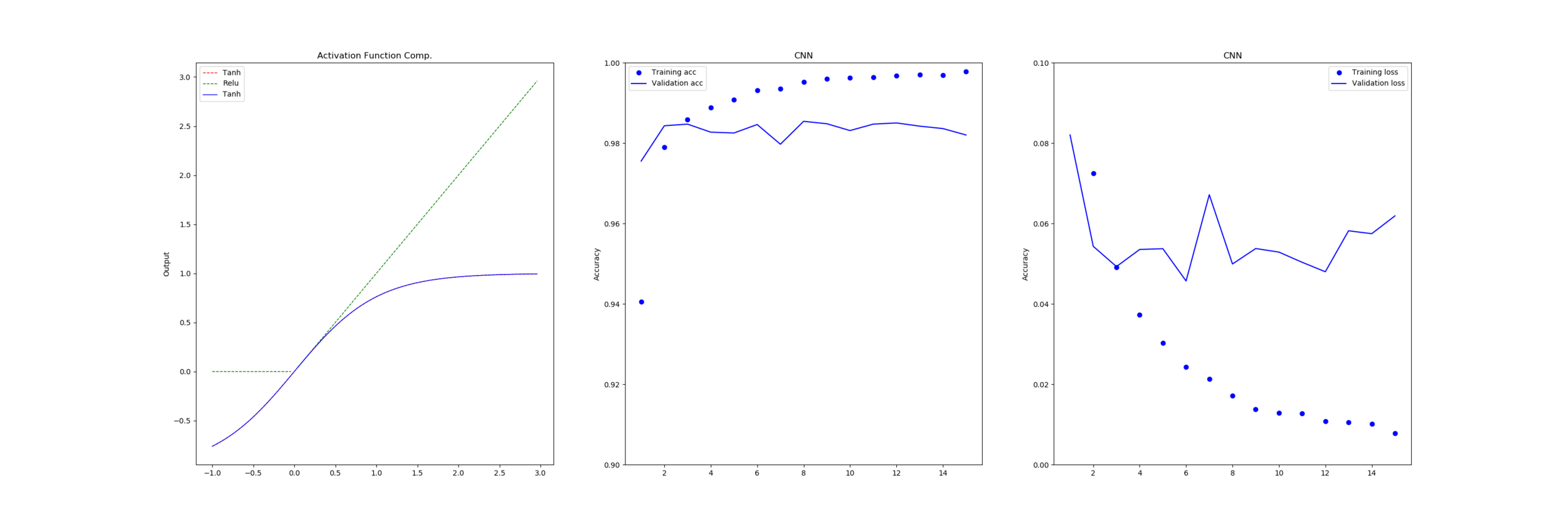
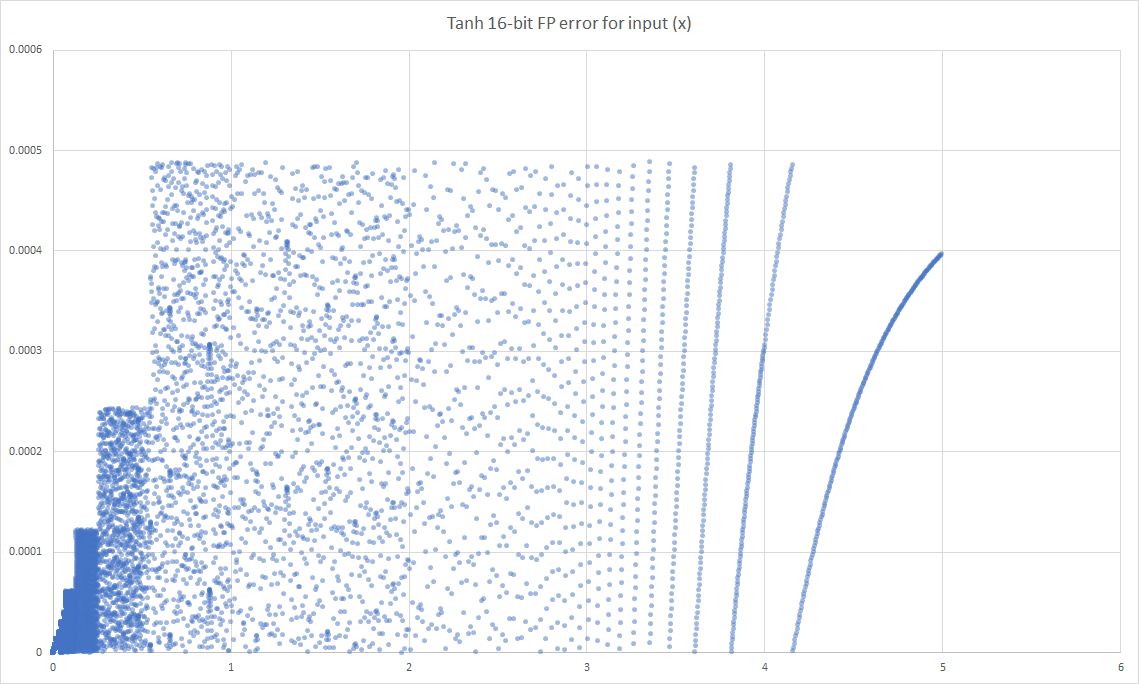
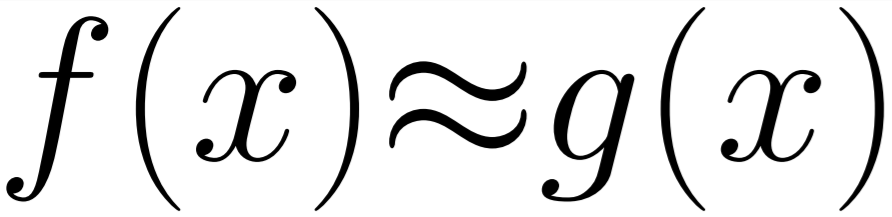We need to as a group of engineers really measure the effectiveness of the solutions we are using for the scale of the task we are doing. If this same approach was used in building construction the end user would be able to see the result - in computing these problems go hidden and are just assumed to be because of the hardware or other problems, when it is a problem that can be improved with a thorough look at the pipeline of the tools, languages and output of our software production process.
Packages, Libraries and Other Junk Drawers
Have you ever had a draw at your desk where you put useful things, some of those would be pulled out and put away frequently, others only now and then, and some things would go into that draw and never removed until you moved desk? Let me introduce you to Python packages.
When we write programs are told to not “reinvent the wheel” - if a solution exists already and it is proven to be good we should use it. The problem is that in Python, and many other languages which have a shared repository of libraries, when we try and fetch the wheel we also often get the horse and cart too.
If you want to use only a small subset of features from a library you must take the entire package. This increases the complexity of the program. It can now potentially do more. Bad for security, bad for compilation, bad for helpful IDEs.
You have just downloaded a large package to use one function or one type. But due to the nature of some languages which are interpreted/run-time compiled/JIT compiled or just in general compiled at the user side of things, you have just performed the same wasteful and dangerous task for every user, run, or installation of your program (depending on how it is used).
Did your program request version v1.0.1 of the package? But the user only have v1.0.2 installed? Better download hundreds of megabytes of software so you can access that important function you were told not to implement.
Why don’t you just extract that single function or class out of the package and ship that embedded in your own code? Is that allowed in the license? Will that somehow change the licensing of the code you are shipping with? Best not walk into those risky waters - make the user download 300mb of useless code instead.
This sounds hyperbolic, but some small packages in Python have very large downloads most of which are simply dependencies. The used:unused ratio of code is frankly crazy and leads to waste.
We can get around this with compiling libraries into our programs so that only the used code is shipped and other nice things (which happen to have good performance benefits) but then it is all complicated by dynamically linked programs which are unfortunately essential for some use-cases.
Packages also make for complex documentation of code. If you have a large project it is going to happen that some library is used partially for a problem and then due to the library not providing all the functionality that is required for a problem a subset of similar functions will be written for more specific behavior. Now, a new person on the project sees some functions being called and has to dig into a massive project to see if the function is from the library or your own code base. Increasing reader complexity.
An interesting side note about programming and language: English is a writer responsible language, this means that it is responsibility of the writer to provide a valid argument and all evidence in a structured and easy to follow way and connect all the dots. In English a good argumentative paragraph will be formed like
‘A plus B gives C. We know this because A is … and … is b. Therefore A plus B must give C.’
This is a property of language that doesn’t exist in some other languages. Unfortunately it appears coding is one of the ones without this property and as a result if everything is not strictly defined it can be very difficult for a person reading code for the first time to know for certain that A, B and C have any relation and if they do - what that relation is or where it is defined.
Exponential Code Complexity By Line
Let’s propose a new simple low-level coding language. It will have a small number of instructions, a single fixed type, 6 fixed register variables and will be used to solve simple maths problems.
Our instructions:
Our type: Float64
Our registers: INPUT0, INPUT1, INPUT2, x, y, z
Example program:
f(x,y,z) = y * x + z
1: STORE INPUT0 , x
2: STORE INPUT1 , y
3: STORE INPUT2 , z
4: MUL x , y, i
5: ADD i , z, i
6: STORE i , RETURNVAL
This results in a simple language that can do simple things.
Now, I want to know how likely it is that the example program above is correct. One way we can look at this is to consider each line in the program a decision.
The first line could be any one of our 3 instructions with any combination of possible inputs for them. This gives ADD and MUL 214 possible combinations of register inputs and STORE 30 possibilities (36 - 6 for the six assignments to itself which would be invalid).
If we were asked to pick the first line at random we would have a 1/458 or 0.2% change of guessing the correct first line. However, the first three lines are order independent so the first line guess odds go up to 3/458.
So what are the odds of generating the whole sequence or a valid version of this sequence?
Lines 1-3 = (3/458 * 2/458 * 1/458). Each line after is 1/458
Line Chance Running Chance
1-3 6 * (1/458^3) 6 * (1/458^3)
4 1/458 6 * (1/458^4)
5 1/458 6 * (1/458^5)
6 1/458 6 * (1/458^6)
This means we would have to run up to 1.5 * 10^15 iterations to brute force find even this simple function. The fact that this number increases so quickly is the reason that most state for function synthesis to be an impossible problem.
However, humans perform function synthesis everyday so the complexity of the problem can’t be this high for a simple problem. We simply haven’t provided enough constraints. A human implementing this simple function would not be trying to produce the entire function in one step. They would approach the problem as setup phase, work phase and return phase, or something more complicated with real world knowledge of the problem we can’t provide to the computer. If we adjust our program to match this phase setup we get:
#SETUP
1.1: STORE INPUT0 , x
1.2: STORE INPUT1 , y
1.3: STORE INPUT2 , z
#WORK
2.1: MUL x , y, i
2.2: ADD i , z, i
#RETURN
3.1: STORE i , RETURNVAL
At each phase we are guaranteeing that the phase before has completed correctly, this gives us an additive rather multiplicative association between the phases.
Line Chance
Phase 1 6 * (1/458^3)
Phase 2 1/(458^2)
Phase 3 1/458
Total 6 * (1/458^3) + 1/(458^2) + 1/458 = 0.00218823582
In this configuration we only need to do approximately 457 iterations to find the correct solution. A ridiculous improvement over our original outlook by validating the steps as we go along.
If we were a human programmer and writing this function and wanted to validate the behavior by debugging we have essentially broken the function into the stages needed to verify the behavior against some test set. This is simplification that humans use all the time when programming.
For this article we are interested in that human behavior, because like the computer a programmer cannot synthesize a new program from scratch it takes steps. We have shown that. So why do we see 1000-line functions in programs?
If you have had any experience with large code bases, you will know that these gargantuan functions and classes are where the bugs creep in, or that unexpected behavior begins after a change elsewhere. The programmer writing or editing that function is having to deal with (choices in the environment)^(† lines in the function) complexity.
This is where what we mentioned about packages comes back. Introducing a large package of functions effectively increases the number of choices in the environment thus drastically reducing the comprehension of larger less isolated functions. This is why we have namespaces and limit the visibility of libraries/modules being included in projects but this is often not managed well and code-bases become incomprehensible to new programmers who don’t have a full idea of the project in their head. This means that changes can’t be safely made because the odds that it was the “correct” line that has been placed is much much lower.
When programs get complex in this way the chances of them being safely changed or optimised is low. It is simply too expensive in programmer time and risk. We need to approach the problem of optimisation from the ground-up in development.
If you don’t believe me - open the chromium project and tell me that you would be confident to be given a task and make a change and be confident that it wouldn’t inadvertently affect another part of the program or introduce a bug.
(† - In reality, not lines but number of operations or decisions)
Conclusions
I am going to conclude these rants here for now and maybe continue with a few more examples of complexity problems effecting performance another time.
To wrap it all up: We are using abstractions which are resulting inefficient code being deployed at a large scale. This inefficiency is coming not only from the languages we use, but how we use them from a lack of understanding of how mistakes and sub-optimal choices are being made. If we don’t begin to produce high-quality scale-able code now, we are going to hit a wall where performance increases wont be possible at the scale we require and that will require a tremendous amount of work to rebuild under higher pressure than we have now. And high-pressure coding doesn’t get the best results either…